~ 12 минут
Что такое эмбеддинги для разработчиков и как они помогают искусственному интеллекту
760
05.11.2023
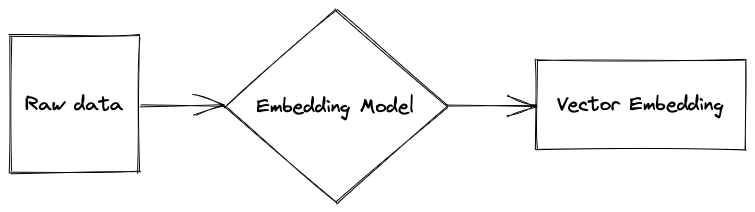
Векторные вложения - это способ представления данных в виде векторов, которые сохраняют семантическую связь между данными. Они широко используются в машинном обучении для различных задач, таких как поиск, обработка естественного языка и компьютерное зрение.


Возможно, вы еще этого не знаете, но векторные встраивания или эмбеддинги (Vector Embeddings) есть везде. Они являются строительными блоками многих алгоритмов машинного и глубокого обучения, используемых различными приложениями - от поиска до помощников с искусственным интеллектом. Если вы рассматриваете возможность создания своего собственного приложения в этой области, вы, скорее всего, в какой-то момент столкнетесь с векторными встраиваниями. В этом посте мы попытаемся получить базовое представление о том, что такое векторные встраивания и как их можно использовать.
Какую проблему мы пытаемся решить?
Когда вы создаете традиционное приложение, ваши структуры данных представляются в виде объектов, которые, вероятно, берутся из базы данных. Эти объекты обладают свойствами (или столбцами в базе данных), которые имеют отношение к создаваемому вами приложению.
Со временем количество свойств этих объектов растет — до такой степени, что вам, возможно, потребуется более тщательно выбирать, какие свойства вам нужны для выполнения данной задачи. Возможно, в конечном итоге вы даже создадите специализированные представления этих объектов для решения конкретных задач, не оплачивая накладные расходы, связанные с обработкой очень “раздутых” объектов. Этот процесс известен как разработка функций — вы оптимизируете свое приложение, выбирая только основные функции, относящиеся к текущей задаче.
Когда вы имеете дело с неструктурированными данными, вам придется пройти через тот же процесс разработки функций. Однако неструктурированные данные, вероятно, содержат гораздо больше подходящих функций, и выполнение ручного проектирования функций неизбежно окажется неприемлемым.
В этих случаях мы можем использовать векторные вложения как форму автоматической разработки объектов. Вместо того чтобы вручную выбирать необходимые функции из наших данных, мы применяем предварительно обученную модель машинного обучения, которая позволит создать более компактное представление этих данных, сохранив при этом то, что имеет смысл в данных.
Что такое векторые вложения
Прежде чем мы углубимся в познания, что такое векторные вложения, давайте поговорим о векторах. Вектор - это математическая структура, имеющая размер и направление. Например, мы можем думать о векторе как о точке в пространстве, причем “направление” представляет собой стрелку от (0,0,0) до этой точки в векторном пространстве.
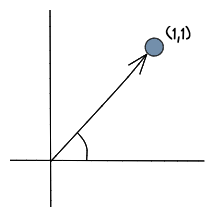
Разработчикам, возможно, было бы проще представить себе вектор как массив, содержащий числовые значения. Например:
vector = [0,-2,...4]
Когда мы смотрим на группу векторов в одном пространстве, мы можем сказать, что некоторые из них ближе друг к другу, в то время как другие находятся далеко друг от друга. Может показаться, что некоторые векторы группируются вместе, в то время как другие могут быть разреженно распределены в пространстве.
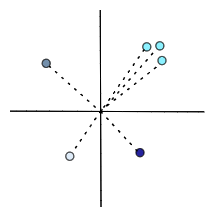
Вскоре мы рассмотрим, как эти взаимосвязи между векторами могут быть полезны.
Векторы являются идеальной структурой данных для алгоритмов машинного обучения — современные процессоры оптимизированы для выполнения математических операций, необходимых для их обработки. Но наши данные редко представляются в виде векторов. Именно здесь в игру вступает векторное встраивание. Это метод, который позволяет нам брать практически любой тип данных и представлять их в виде векторов.
Но это не так просто, как просто преобразовать данные в векторы. Мы хотим быть уверены, что сможем выполнять задачи с этими преобразованными данными без потери первоначального значения данных. Например, если мы хотим сравнить два предложения — мы хотим сравнить не просто слова, которые они содержат, а скорее то, означают ли они одно и то же или нет. Чтобы сохранить значение данных, нам нужно понять, как создавать векторы, в которых отношения между векторами имеют смысл.
Чтобы сделать это, нам нужно то, что известно как модель встраивания. Многие современные модели встраивания строятся путем передачи большого объема помеченных данных в нейронную сеть. Возможно, вы уже слышали о нейронных сетях раньше — они также являются популярным инструментом, используемым для решения всевозможных сложных задач. Говоря очень простыми словами, нейронные сети состоят из слоев узлов, соединенных функциями. Затем мы обучаем эти нейронные сети выполнять всевозможные задачи.
Мы обучаем нейронные сети, применяя контролируемое обучение — передавая в сеть большой набор обучающих данных, состоящий из пар входных данных и помеченных выходных данных. В качестве альтернативы мы можем применить самоконтрольное или неконтролируемое обучение, любое из которых не требует маркированных результатов. Эти значения преобразуются при каждом уровне сетевых активаций и операций. С каждой итерацией обучения нейронная сеть изменяет активации на каждом уровне. В конечном счете, он может предсказать, какой должна быть выходная метка для данного входного сигнала — даже если он раньше не видел этот конкретный входной сигнал.
Модель встраивания - это, по сути, нейронная сеть с удаленным последним слоем. Вместо того, чтобы получать конкретное помеченное значение для входных данных, мы получаем векторное вложение.
Отличным примером модели встраивания является популярный word2vec, который регулярно используется для широкого спектра текстовых задач. Давайте взглянем на визуализацию, созданную с помощью инструмента TensorFlow projector, который позволяет легко визуализировать вложения.
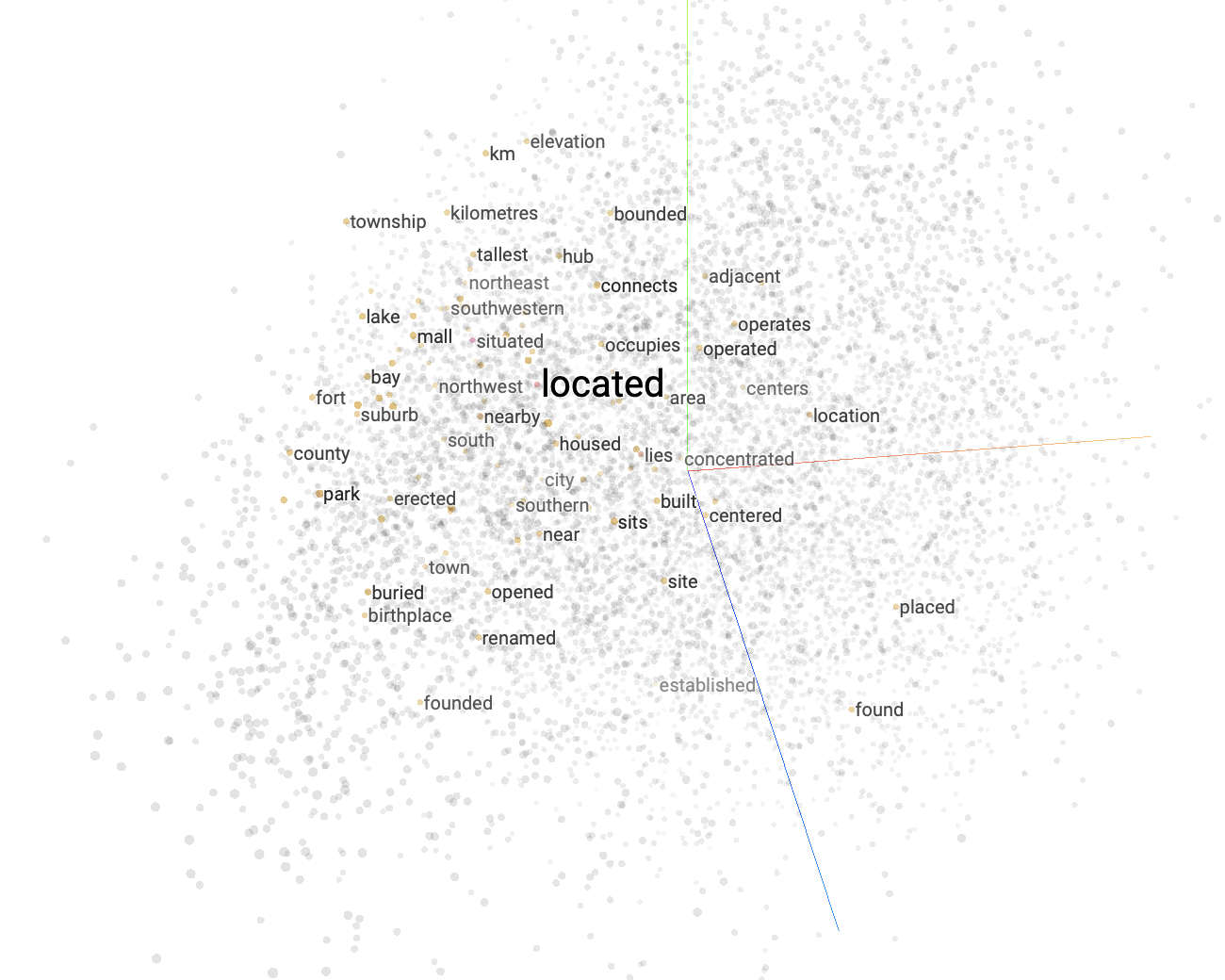
Хотя эта визуализация представляет только три измерения встраиваний, она может помочь нам понять, как работает модель встраивания. В визуализации выделено несколько точек данных, каждая из которых представляет собой векторное вложение для слова. Как следует из названия, word2vec встраивает слова. Слова, которые кажутся близкими друг к другу, семантически схожи, в то время как слова, расположенные далеко друг от друга, имеют разные семантические значения.
После обучения модель встраивания может преобразовать наши необработанные данные в векторные встраивания. Это означает, что он знает, где размещать новые точки данных в векторном пространстве.
Как мы видели с word2vec, в контексте модели векторы, расположенные близко друг к другу, имеют контекстуальное сходство, в то время как векторы, расположенные далеко друг от друга, отличаются друг от друга. Это то, что придает нашему вектору значение — его взаимосвязь с другими векторами в векторном пространстве зависит от того, как модель внедрения “понимает” предметную область, на которой она была обучена.
Что я могу сделать с векторными вложениями?
Векторные вложения - невероятно универсальный инструмент, который может быть применен во многих областях. Вообще говоря, приложение будет использовать векторное вложение в качестве своего запроса и создавать другие векторные вложения, которые похожи на него, с соответствующими значениями. Разница между приложениями каждой предметной области заключается в значимости этого сходства.
Вот несколько примеров:
- Семантический поиск - поисковые системы традиционно работают путем поиска совпадений ключевых слов. Используя векторные вложения, семантический поиск может выходить за рамки подбора ключевых слов и выдавать результаты на основе семантического значения запроса.
- Приложения, отвечающие на вопросы - обучая модель встраивания парам вопросов и соответствующим ответам, мы можем создать приложение, которое отвечало бы на вопросы, которые ранее не встречались.
- Поиск изображений - векторные вложения идеально подходят для того, чтобы служить основой для задач поиска изображений. Существует множество готовых моделей, таких как CLIP, ResNet и другие. Различные модели справляются с различными типами задач, такими как сходство изображений, обнаружение объектов и многими другими.
- Поиск аудио - преобразуя аудио в набор активаций (звуковую спектрограмму), мы создаем векторные вложения, которые можно использовать для поиска сходства звука.
- Рекомендательные системы - мы можем создавать вложения из структурированных данных, которые соотносятся с различными объектами, такими как товары, статьи и т.д. В большинстве случаев вам пришлось бы создать свою собственную модель встраивания, поскольку она была бы специфична для вашего конкретного приложения. Иногда это может сочетаться с неструктурированными методами встраивания, когда найдены изображения или текстовые описания.
- Обнаружение аномалий - мы можем создавать вложения для обнаружения аномалий, используя большие наборы данных с маркированной сенсорной информацией, которые идентифицируют аномальные явления.
Векторные встраивания невероятно эффективны, и это ни в коем случае не исчерпывающий список — ознакомьтесь с нашим разделом примеров приложений, чтобы углубиться в него. Вы также можете прочитать больше об основах векторного поиска, чтобы узнать, как Pinecone может помочь вам разобраться с векторными вложениями.
Источник: https://www.pinecone.io/learn/vector-embeddings-for-developers/
Взгляните на наш стартап:

Выбирай экскурсии и активности по всему миру
Уже зарегистрировано 0 стран, 0 направлений, 0 экскурсий
Есть интересная идея?
И вы очень хотите ее реализовать, пишите нам и получите подробное коммерческое предложение и быструю реализацию



